学校での成績評価や会社での人事評価といったように、評価というのは、社会で生きる人々にとって常について回るものですね。しかし、評価するというのは、身近でありながら案外難しいことではないでしょうか?
重要なひとつの点で優れていればいいのか、あるいは全体的にバランスよく優れていることに対して高い評価をつける方がいいのか。客観的で一貫性のある評価をするには評価の基準、評価指標が必要です。
そしてそれは、機械学習のモデルも同様です。機械学習のモデルを作成した際に、そのモデルがどれくらい「良い」モデルなのかを判断するためには、評価指標を決めて判断しなければなりません。ということで、本稿では、機械学習の評価指標(分類編)と題し、分類問題に対する機械学習モデルの評価指標について、解説していきます。
評価指標とは
本節では、評価指標を用いる目的と、評価指標を理解するための重要な前提知識として、混同行列(Confusion Matrix)についてご説明します。
評価指標を用いる目的
本稿でご紹介する評価指標は、機械学習で分類問題を解く際に、機械学習モデルによる予測を評価するための指標です。冒頭で述べたように、物事は常に1つの基準で評価できるわけではありません。機械学習による分類問題も例外ではなく、その分類の目的に応じて、評価指標を使い分ける必要があります。分類の目的と評価指標の選び方に関しては、後ほど詳述します。
混同行列(Confusion Matrix)
評価指標の詳細な説明に入る前に、混同行列というものについてご説明します。混同行列とは、2値分類問題において、予測と実際の分類を行列形式にまとめたものです。
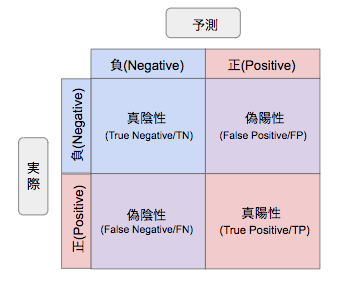
ウイルス検査を例に、表の各マスを順に説明します。なお、ウイルス検査における「予測」とは、検査結果のことで、「実際」とは、実際にその人が陽性であるか陰性であるかを指します。
- 真陰性(True Negative, TN):検査で陰性とされ、実際に陰性である場合
- 偽陰性(False Negative, FN):検査で陰性とされたものの、実際には陽性である場合
- 偽陽性(False Positive, FP):検査で陽性とされたものの、実際には陰性である場合
- 真陽性(True Positive, TP):検査で陽性とされ、実際に陽性である場合
※なお、負(Negative)が正(Positive)よりも先に書かれている点に違和感を感じる方もいらっしゃるかもしれませんが、このような行列になっているのは、この混同行列が後のPythonでの実装の際に出てくる混同行列の表示に対応しているためです。
理解を深めるため、もう一つ具体例をあげましょう。みなさん、レタスとキャベツを見分けられずに困ったことはないでしょうか?料理をされる方にとってはなんてことないと思いますが、普段あまり料理をしない筆者は、度々レタスとキャベツを間違えることがあります。さて。今、Aさんの目の前にレタスとキャベツが計100個あるものの、それぞれ何個ずつあるかはわからないとします。Aさんはそれらを分類するため、1つ1つじっくり観察して、70個がキャベツ、30個がレタスであると予測しました。

しかし、実際にはキャベツと予想した70個のうち、実際にキャベツであったのは20個、レタスと予想した30個のうち、実際にレタスであったのは10個でした。この場合、混同行列は以下のようになります。(この例では、便宜的にキャベツを正、レタスを負としますが、もちろん逆でも構いません。その場合にはまた別の混同行列になります。)
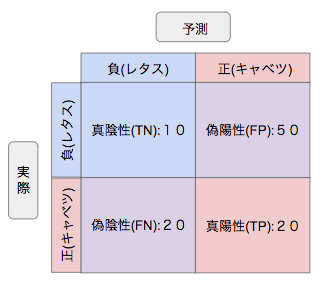
混同行列については、お分かりいただけたかと思います。分類の評価指標は、この混同行列の各マスの値から特定のものを選び、演算することによって作られています。次の節で、各種評価指標について解説していきます。
各種評価指標の解説
本節では、上記のレタスとキャベツの例を活用して、各種評価指標の算出方法とその特徴を詳細に説明していきます。
- 正解率 (Accuracy)
- 適合率 (Precision)
- 再現率 (感度, Recall, True Positive Rate, TPR)
- F値 (F-measure)
- 特異度 (specificity, True Negative Rate, TNR)
- 偽陽性率 (False Positive Rate, FPR)
- Log Loss
- AUC(ROC曲線、PR曲線)
正解率 (Accuracy)
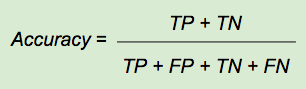
まずは、正解率(Accuracy)について解説します。正解率とは、その名の通り「全ての予測のうち、正解した予測の割合」を指します。非常にシンプルで直感的にも解釈しやすい指標です。レタスとキャベツの例で具体的に計算してみましょう。Aさんの予測の正解率は30/100=0.3となります。みなさんがおそらく直感的に感じておられるように、Aさんの予測能力の低さが適切に表現されているといえるでしょう。しかし、例えば機械の異常検知など、ほとんどがNegativeで稀にPositiveが出現するような、偏りが大きいデータを扱う場合にはあまり有効な評価指標とは言えません。この点については、後半の実装にて実際にデータを扱ってご説明します。
適合率 (Precision)
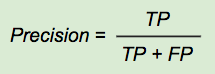
次に解説するのは適合率(Precision)です。適合率は、「陽性と予測したもののうち、実際に陽性であるものの割合」を表す指標です。適合率は、FPを小さくすることを重視する指標なので、誤って陽性と判断しては困る場合に用いると有効です。例えば、レタスとキャベツの例で計算すると、20/70≒0.29です。Aさんの予測精度の低さが適合率からも分かりますね。一方、適合率の弱点は陰性の予測を無視している点です。つまり、どれだけ偽陰性の予測を出しても、適合率には反映されません。偽陰性が多いことが問題になるケースでは、用いないほうがいいでしょう。
再現率 (感度, Recall, True Positive Rate, TPR)

呼び方が複数あってややこしいのが、再現率 (感度、Recall, True Positive Rate, TPR)です。True Positive Rateと覚えるのが最も直感的に分かりやすいですが、後ほど他の指標の説明の際にRecallも出てくるので覚えておきましょう。再現率は、「実際に陽性であるもののうち、正しく陽性と予測できたものの割合」です。再現率は、適合率と対照的な指標で、FNを小さくすることを重視する指標となっています。ゆえに、誤って陰性と判断しては困る場合に用いられます。レタスとキャベツの例で計算すると、20/40=0.5となりました。つまり、Aさんの予測は「キャベツを誤ってレタスと判断してしまう割合」という観点からは、これまでの他の指標よりもいい評価が得られるようです。また、再現率は適合率と対照的な指標であるため、適合率の長所が再現率の短所となります。つまり、再現率は偽陽性(FP)を無視する指標であるため、やたらめったら陽性判定をしてたくさん偽陽性を出したとしても、再現率が下がることはありません。偽陽性が多いと困る場合には重視しない方が賢明と言えるでしょう。
F値 (F-measure, F1値, F1-measure)

次はF値について説明します。F値は対照的な特徴を持つ適合率と再現率の調和平均です。簡単に言えば、対照的な両者の特徴をバランスよく含んでいる指標と言えます。分子が適合率と再現率の積になっているため、片方が極端に低い場合に、正しく低い評価をつけることができるのです。言い換えれば、偽陽性や偽陰性が極端に多い場合には、値が小さくなるため、どちらの指標もそれなりに高い値である必要があります。値の範囲はこれまでの指標と同様に0~1で、1に近づくほど予測性能がいいということになります。レタスとキャベツの例でF値を計算してみると、約0.36となりました。やはり、適合率が低いためF値も低く出ています。
特異度 (specificity, True Negative Rate, TNR)

次に解説するのは特異度 (specificity, True Negative Rate, TNR)です。特異度は、「実際に陰性であるもののうち、正しく陰性と予測できたものの割合」を表します。再現率の正負を反転させた指標ですね。特徴としては、適合率と同じようにFPが小さければ小さいほど値が大きくなるため、偽陽性を減らすことを重視する際に用いると良いと言えるでしょう。レタスとキャベツの例では偽陽性が多いため、特異度は10/60≒0.17と非常に低くなっています。
偽陽性率 (False Positive Rate, FPR)

本節の前半最後にご紹介する評価指標が、偽陽性率(False Positive Rate, FPR)です。偽陽性率は、「実際には陰性であるもののうち、誤って陽性と予測したものの割合」です。これまでの指標と異なり、小さければ小さいほどいい指標です。また、式を特異度と見比べるとお分かりになると思いますが、偽陽性率は「1 ー (特異度)」で求めることもできます。レタスとキャベツの例では、約0.83と非常に高い値になっています。
Column : PCR検査の性能は?
「ウイルス検査」、「偽陽性」などと聞くと真っ先に思い浮かべるのは、新型コロナウイルスの検査であるPCR検査ではないでしょうか。PCR検査の性能がどれくらいなのか、気になっている方は多いと思います。一般社団法人日本疫学会によると、PCR検査の感度(=再現率、実際にウイルスに感染している人のうち、検査で陽性と判定される割合)として一番よい値になるのは、「感染から8日目(症状発現の3日後)の80%」とのことです。すなわち、最も感染者を検出しやすいタイミングでも、感染者のうち20%は陰性と判定してしまうことになります。このように、評価指標についての知識があると様々な場面で活かせるので、数は多いですが1つずつ理解していきましょう。
Log Loss
さて、ここから本節の後半ということで、さらに2つの評価指標について解説していきます。1つ目が、Log Lossです。これは、端的に言うと、前述の正解率(Accuracy)に確率を導入した指標です。Log Lossも正解率と同様に、全ての予測を評価する指標です。しかし、正解率の考え方に確率を導入することによって、分類の予測を正解・不正解だけでなく、正解・不正解との距離を含めて評価することができます。なお、Log Lossは小さければ小さいほどモデルの性能がいいことを示します。それでは、具体例をあげましょう。正解が1であるデータに対して、2つの分類モデルで予測したところ、どちらも0と予測してしまったとします。しかし、それらのモデルが予測した確率を確認したところ、以下の表の通りだったとしましょう。
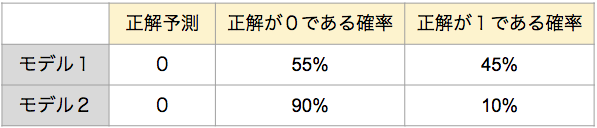
表を見ると、モデル1の方が正解に近かったと言うことができそうですね。他のデータに適用した際に正しい予測ができる確率はモデル1の方が高そうです。そしてこの場合、正解率はどちらも同じになりますが、Log Lossはモデル1の方が小さくなり、モデル1の方が優れていると評価することができます。このように、Log Lossはモデルを正解率より詳細に評価したい際に用いると有効だと言えます。
AUC(Area Under the Curve)
本節最後の評価指標が、AUC(Area Under the Curve)です。AUCは名前の通り、ある曲線の下側の面積の大きさで分類予測を評価する指標です。面積は0から1の範囲で変動し、AUCが大きいほど優れた予測だと言うことができます。ここでは、AUCを算出するための曲線として、以下の二つについて解説します。なお、これらの曲線がどのようにして描かれているのかについては後半の実装の際に詳しく解説しますので、とりあえず概要だけ覚えておいてください。
AUC(ROC曲線)
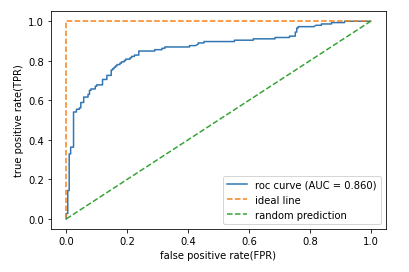
一つ目が、ROC曲線です。ROC曲線は、横軸に偽陽性率(false positive rate,FPR)を、縦軸に再現率(Recall, true positive rate, TPR)をとる曲線です。
AUC(PR曲線)
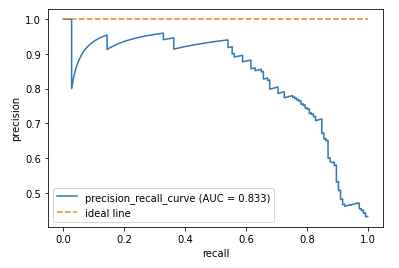
2つ目が、PR曲線です。PR曲線は名前の通り、縦軸に適合率(Precision)を、横軸に再現率(感度, Recall,true positive rate,TPR)をとる曲線です。PR曲線には、偏りが大きいデータに対する予測も適切に評価できるという特徴があります。偏りが大きいデータの例として、工場における機械の故障検知などが挙げられるでしょう。故障をPositive、正常な状態をNegativeとして、データを取って機械が故障していないかを観測しているとします。まともな機械を使っていればほとんどのデータがNegativeとなるでしょうが、このようなデータを用いた予測を評価するのは容易ではありません。このような場合に、PR曲線におけるAUCが用いられるのです。
さて、いかがでしたでしょうか?これで、主な評価指標の概要についてはご理解いただけたかと思います。全ての特徴を覚えて使いこなすのは容易ではありませんので、次節の実装を通して、さらに理解を深めていきましょう。
実装その1:ロジスティック回帰による分類で評価指標を確認
本節では、ロジスティック回帰で分類を実装した上で、各種指標を実際に算出していきましょう。本稿では、Google Colabを用いて実装していきます。本稿は2020年8月28日時点でコードの実行確認を行いましたので、Google Colabのデフォルトのバージョンが変更されない限り、ライブラリをそのままインポートすれば同じように実装可能です。ぜひ、ご自身でも実装してみてください。(参考:Google Colabの使い方)
ロジスティック回帰による分類
それでは、評価指標を確認するために、まずはロジスティック回帰で簡単な分類を行いましょう。
はじめに、必要なライブラリを読み込みます。
|
1 2 3 4 5 6 7 8 9 10 11 |
[In ]: #ライブラリの読み込み import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline |
本稿では、ご存知の方も多いであろうKaggleのtitanicデータを用いて、生存したか否かを示す survived の値を予測するために、ロジスティック回帰モデルを実装していきます。titanicのデータセットはseaborn上に用意されているので、今回はそれを活用しましょう。
|
1 2 3 4 5 6 7 8 |
[In ]: #titanicデータセットを読み込んで、一部を表示 df = sns.load_dataset('titanic') df.head() |
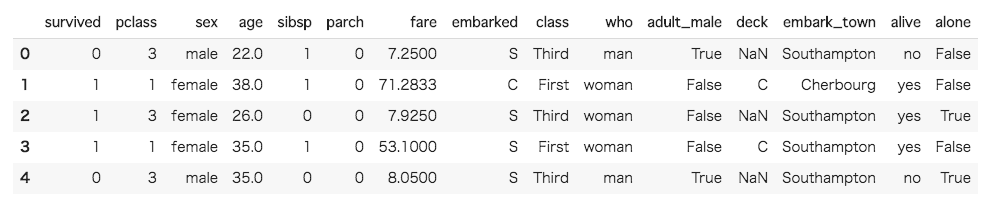
早速最初の5行を表示してみました。alive という変数が survived に連動している可能性がありそうですね。今回は高い精度の分類をすることが目的ではないので、残しておいても問題はないかもしれませんが除外してしまいましょう。その前に、各行の欠損値の有無も確認しておくことにします。
|
1 2 3 4 5 6 7 |
[In ]: #欠損値の有無を確認 df.isnull().sum() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
[Out ]: survived 0 pclass 0 sex 0 age 177 sibsp 0 parch 0 fare 0 embarked 2 class 0 who 0 adult_male 0 deck 688 embark_town 2 alive 0 alone 0 dtype: int64 |
deck という変数が格納されている列にかなり多くの欠損値があるようですね。この列と、先ほどの alive をまとめて除外してしまいましょう。さらに、欠損値を含む行も削除します。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
[In ]: #余計な変数を除外 drop_list = ["deck","alive"] df = df.drop(drop_list, axis=1) #欠損値を含む行を削除して、表示 df = df.dropna() df |
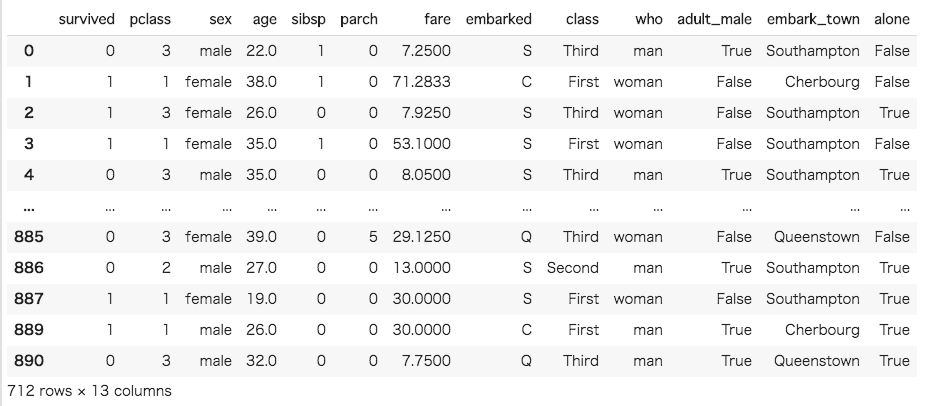
ここからは、モデル構築の準備に入ります。まず、データを特徴量とターゲットに分割しましょう。今回のターゲットは survived なので、特徴量は survived 以外の変数ということになります。(参照:特徴量とは?)
|
1 2 3 4 5 6 7 8 |
[In ]: #データを特徴量とターゲットに分割 X = df.drop("survived",axis=1) Y = df["survived"] |
次に、特徴量のデータセットには多くのカテゴリカル変数が含まれているため、これらをダミー変数化して、中身を確認します。
|
1 2 3 4 5 6 7 8 |
[In ]: #特徴量のカテゴリカル変数をダミー変数化し、確認 X = pd.get_dummies(X) X.head() |

問題なくデータを整形することができました。一応ターゲットのデータも確認しておきます。
|
1 2 3 4 5 6 7 |
[In ]: #ターゲットを確認 Y.head() |
|
1 2 3 4 5 6 7 8 9 10 11 |
[Out ]: 0 0 1 1 2 1 3 1 4 0 Name: survived, dtype: int64 |
次に、特徴量とターゲットのデータの両方を、ロジスティック回帰モデルを構築するための訓練データと、モデルの性能を確認するためのテストデータに分割します。そのために、scikit-learnのtrain_test_splitを活用します。再現性を担保するためrandom_state引数を指定しておきます。
|
1 2 3 4 5 6 7 8 |
[In ]: #特徴量とターゲットを、訓練データとテストデータに分割 from sklearn.model_selection import train_test_split X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=0.5,random_state=0) |
それぞれのデータの大きさを確認しておきましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
[In ]: #データの確認 print("X.shape:",X.shape) print("X_train.shape:",X_train.shape) print("X_test.shape:",X_test.shape) print("Y.shape:",Y.shape) print("Y_train.shape:",Y_train.shape) print("Y_train.shape:",Y_train.shape) |
|
1 2 3 4 5 6 7 8 9 10 11 |
[Out ]: X.shape: (712, 21) X_train.shape: (356, 21) X_test.shape: (356, 21) Y.shape: (712,) Y_train.shape: (356,) Y_train.shape: (356,) |
712行21列の特徴量と、712行1列のターゲットがどちらも356行ずつに正しく分割されていることが分かります。
では、ロジスティック回帰モデルのインスタンスを作成し、訓練データで学習させましょう。なお、デフォルトの100回のイテレーションではwarningが出るため、max_iter引数を1000と指定します。
|
1 2 3 4 5 6 7 8 9 |
[In ]: #ロジスティック回帰モデルのインスタンスを作成し、訓練データで学習 from sklearn.linear_model import LogisticRegression lr = LogisticRegression(max_iter=1000, random_state=0) lr.fit(X_train,Y_train) |
|
1 2 3 4 5 6 7 8 9 10 |
[Out ]: LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True, intercept_scaling=1, l1_ratio=None, max_iter=1000, multi_class='auto', n_jobs=None, penalty='l2', random_state=0, solver='lbfgs', tol=0.0001, verbose=0, warm_start=False) |
学習が終了したら、テストデータを使って、モデルからYの値を予測して出力します。
|
1 2 3 4 5 6 7 8 |
[In ]: #モデルからYの値を予測して出力 Y_pred = lr.predict(X_test) print(Y_pred) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
[Out ]: [1 0 1 0 0 0 1 0 0 1 1 1 1 0 0 1 0 1 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 1 1 1 1 0 0 1 0 0 0 0 0 0 1 0 0 1 1 1 1 0 1 1 0 0 1 0 0 0 0 1 0 0 1 0 1 1 0 1 1 0 0 0 1 0 0 0 0 1 0 1 1 0 0 0 1 0 0 0 0 1 1 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 1 1 1 1 1 0 0 0 1 0 1 1 1 0 0 0 0 0 0 0 1 1 1 0 0 1 1 1 1 0 1 0 0 0 0 0 0 0 1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 1 1 0 1 1 0 0 1 1 0 1 0 1 0 0 0 0 0 0 1 0 1 0 0 0 1 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 0 0 0 0 0 1 0 0 0 1 0 0 1 0 1 0 0 1 1 1 1 1 0 1 1 1 0 0 1 0 1 1 0 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 0 0 0 0 0 0 1 0 0 1 1 1 1 0 1 0 0 1 1 0 1 0 1 0 1 1 0 0] |
0と1の二値変数で、Yの予測値が出力されました。
各種評価指標の算出
上で求めた予測値とテストデータの実際の値を用いれば各評価指標を計算することが可能です。当然ですが手計算をしていたら日が暮れてしまいますので、評価指標を求めることができる便利なツールをscikit-learnからインポートして、評価指標を求めてみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
[In ]: #混同行列、正解率、適合率、再現率、F値を表示 from sklearn.metrics import confusion_matrix, accuracy_score, precision_score,recall_score,f1_score print('confusion matrix = \n', confusion_matrix(y_true = Y_test, y_pred = Y_pred)) print('accuracy = ',accuracy_score(y_true = Y_test , y_pred = Y_pred)) print('precision = ',precision_score(y_true = Y_test , y_pred = Y_pred)) print('recall = ',recall_score(y_true = Y_test , y_pred = Y_pred)) print('f1 score = ',f1_score(y_true = Y_test , y_pred = Y_pred)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
[Out ]: confusion matrix = [[179 31] [ 40 106]] accuracy = 0.800561797752809 precision = 0.7737226277372263 recall = 0.726027397260274 f1 score = 0.7491166077738517 |
混同行列と各種評価指標を求めて表示することができました。混同行列は、本稿冒頭の混同行列の説明の際に示した図と同じ順で表示されています。それぞれの値を確認すると、survived の値をまずまずうまく予測できていることが分かります。さて、続いてLog lossを算出してみましょう。Log lossは確率を入力として分類手法の性能を評価します。ですのでまず、モデルからYが0、1である確率を予測して、一部を表示してみましょう。ロジスティック回帰モデルから、ターゲットが0と1に分類される確率をそれぞれ出力したい場合には、predict_probaメソッドを用います。
|
1 2 3 4 5 6 7 8 |
[In ]: #モデルから、Yが0、1である確率を予測して5行目まで出力 probs = lr.predict_proba(X_test) print(probs[:5]) |
|
1 2 3 4 5 6 7 8 9 10 |
[Out ]: [[0.48101474 0.51898526] [0.80039621 0.19960379] [0.02368652 0.97631348] [0.8534331 0.1465669 ] [0.94125991 0.05874009]] |
0列目の値が「Yが0である確率」、1列目の値が「Yが1である確率」の予測値です。
それでは、Log lossを算出してみましょう。
|
1 2 3 4 5 6 7 8 |
[In ]: #Log_lossを算出 from sklearn.metrics import log_loss print('log loss = ', log_loss(y_true=Y_test,y_pred=probs)) |
|
1 2 3 4 5 6 |
[Out ]: log loss = 0.4446113266279786 |
次に、いよいよROC曲線とPR曲線を描き、それぞれのAUCを算出してみましょう。まず、必要なライブラリをインポートします。
|
1 2 3 4 5 6 7 |
[In ]: #必要なライブラリをインポート from sklearn.metrics import roc_curve, precision_recall_curve, auc |
ここで、先ほど後回しにした、AUCを算出するために用いる曲線の描き方についての解説を行います。ROC曲線とPR曲線がありますが、どちらの場合もまず、データがPositive(=1)である確率をモデルから予測して、Positiveである確率が高いと予測したものから順に並べます。そして、予測した確率からPositiveであると判定する基準(=閾値)を上から順に降ろしていった時に、FPRとTPRがどのように変化するかをプロットしたものが、ROC曲線です。また、同様に適合率(Precision)と再現率(Recall,TPR)の変化をプロットしたものがPR曲線です。文字だけでは分かりづらいと思うので、下の例で確認してみましょう。
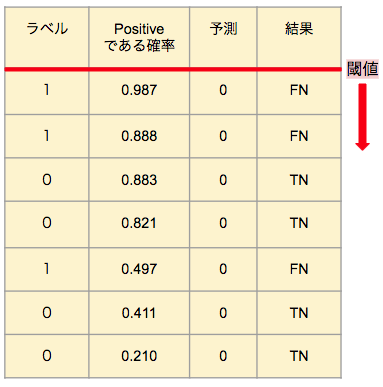
<表1>
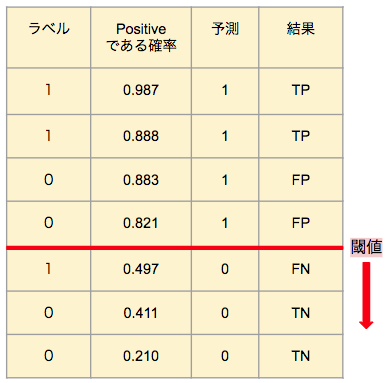
<表2>
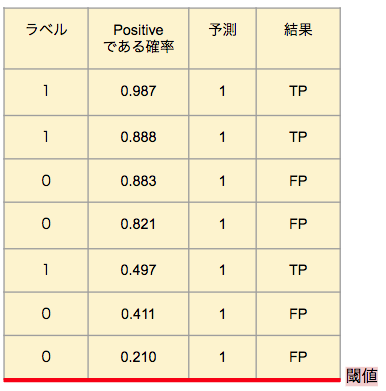
<表3>
これらの表は、7つのデータに対して分類予測を行うケースです。表の左から順に、ラベル(=正解データ)、モデルが導き出した、そのデータがPositiveである確率の予測、モデルによる分類の予測、結果となっています。表から分かるように、Positiveである確率を予測するモデルでは、閾値を定めることで分類の予測を行います。そのため、閾値を変化させつつ、その都度各種評価指標の変化を見ることで、分類予測の性能を細かく確認することができるのです。その変化を可視化したものが、ROC曲線やPR曲線で、性能の評価を数値化したものがAUCです。
では、先ほどのtitanicのデータに戻って、ROC曲線とPR曲線を描き、AUCを算出してみましょう。
|
1 2 3 4 5 6 7 8 |
[In ]: #テストデータがクラス1に属する確率を予測し、その確率からFPR、TPR、閾値を計算 Y_score = lr.predict_proba(X_test)[:,1] fpr, tpr, thresholds = roc_curve(y_true=Y_test,y_score=Y_score) |
閾値の変化に伴う、FPRとTPRの変化を表示してみます。左の列から順にFPR、TPR、閾値となっています。
|
1 2 3 4 5 6 7 8 |
[In ]: #FPR、TPR、閾値をデータフレームに格納して表示 fpr_tpr_thresholds_df = pd.DataFrame([fpr,tpr,thresholds]) fpr_tpr_thresholds_df.T |
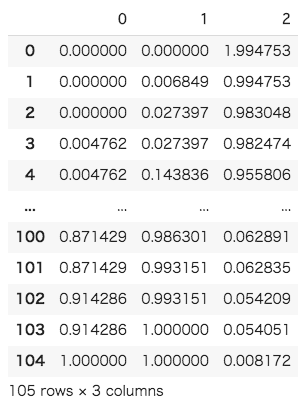
そして、実際にROC曲線を描き、算出したAUCも併せて表示したのが以下の図です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
[In ]: #ROC曲線を描き、AUCを算出 plt.plot(fpr,tpr,label='roc curve (AUC = %0.3f)' % auc(fpr,tpr)) plt.plot([0,0,1], [0,1,1], linestyle='--', label='ideal line') plt.plot([0, 1], [0, 1], linestyle='--', label='random prediction') plt.legend() plt.xlabel('false positive rate(FPR)') plt.ylabel('true positive rate(TPR)') plt.show() |

同様の処理を行ってPR曲線を描くと、以下のようになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
[In ]: #PR曲線を描き、AUCを算出 probas_pred = lr.predict_proba(X_test)[:,1] precision, recall, thresholds = precision_recall_curve(y_true=Y_test, probas_pred=Y_score) plt.plot(recall,precision,label='precision_recall_curve (AUC = %0.3f)' % auc(recall,precision)) plt.plot([0,1], [1,1], linestyle='--', label='ideal line') plt.legend() plt.xlabel('recall') plt.ylabel('precision') plt.show() |

実装その2:大きな偏りのあるデータを用いた予測と、その評価
さて、これで一通り代表的な評価指標を算出し、表示することができました。ここでは、+αの実装として、大きな偏りのあるデータに対する予測と、その評価も行ってみたいと思います。偏りがあるデータの場合、通常のデータに比べて正解率があまり有効な指標でなくなる、ROC曲線よりもPR曲線の方が有効になるなどの違いがあります。ここでの実装を通して、その違いを確認してみましょう。今回は、データに偏りを持たせるため、生存者(survived=1)の数を先ほどの5%に減らすことにします。まず、再度titanicのデータセットを読み込んで、不要な行と列を除外します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
[In ]: #titanicデータセットを読み込んで、一部を表示 df = sns.load_dataset('titanic') df.head() #不要な行と列を除外 drop_list = ["deck","alive"] df = df.drop(drop_list, axis=1) df = df.dropna() |
次に、survivedが1の変数のみを取り出して、仮の変数Aに代入し、そのうちの5%をランダムにサンプリングします。ランダムサンプリングにはsampleメソッドを用います。サンプリングの割合は、frac引数で指定します。
|
1 2 3 4 5 6 7 8 |
[In ]: A = df[df["survived"] == 1] A = A.sample(frac=0.05,random_state=0) A |
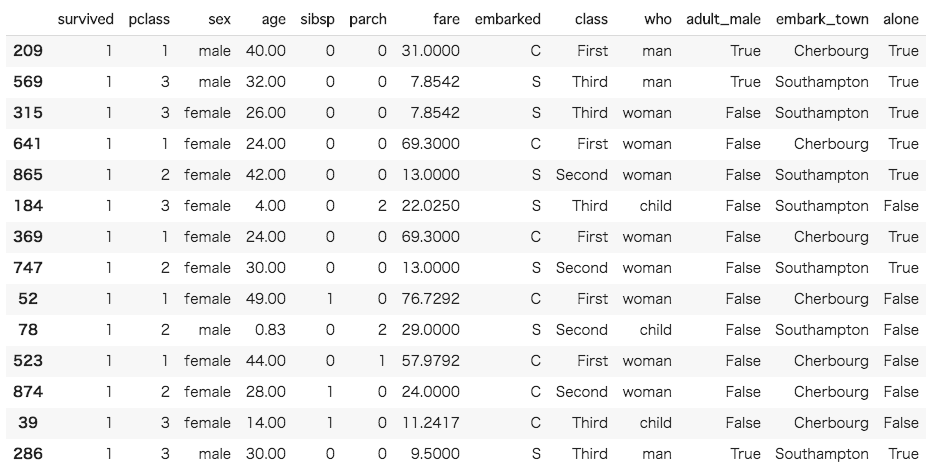
このデータに、データセットから取り出した死亡者のデータを結合し、dfに代入したら、データセットの準備は完了です。データフレームの結合には、concatメソッドを用います。
|
1 2 3 4 5 6 7 8 |
[In ]: B = df[df["survived"] == 0] df = pd.concat([A,B]) df |
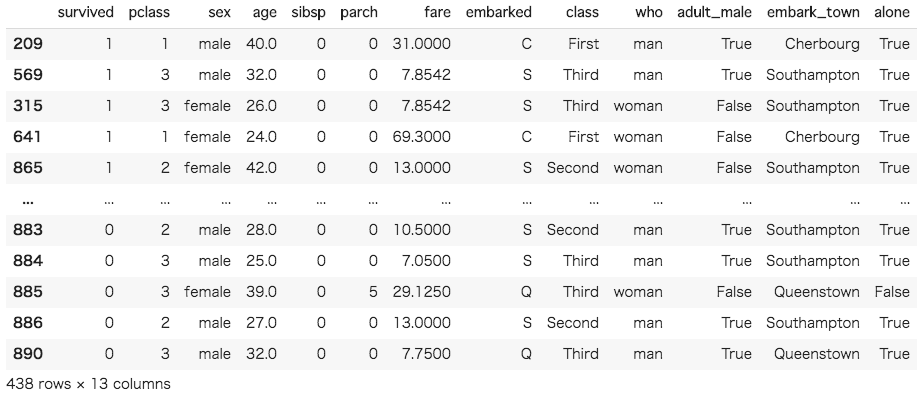
では、先ほどの実装と同様に、データを特徴量とターゲットに分割して、ターゲットのデータを確認してみましょう。なお、データの分割の際に、特徴量のカテゴリカル変数をダミー変数化しています。
|
1 2 3 4 5 6 7 8 9 10 |
[In ]: #データを特徴量とターゲットに分割 X = pd.get_dummies(df.drop("survived",axis=1)) Y = df["survived"] #ターゲットのデータを確認 pd.Series.value_counts(Y) |
|
1 2 3 4 5 6 7 8 |
[Out ]: 0 424 1 14 Name: survived, dtype: int64 |
死亡者424人に対して生存者14人と、データに偏りを持たせることができました。ここから先は、先ほどと同様の手順でロジスティック回帰による分類を行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
[In ]: #特徴量とターゲットを、訓練データとテストデータに分割 X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=0.5,random_state=0) #ロジスティック回帰モデルのインスタンスを作成し、訓練データで学習 lr = LogisticRegression(max_iter=1000,random_state=0) lr.fit(X_train,Y_train) #モデルからYの値を予測して出力 Y_pred = lr.predict(X_test) print(Y_pred) |
|
1 2 3 4 5 6 7 8 9 10 11 |
[Out ]: [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] |
ロジスティック回帰により分類を行いました。なお、TrueとFalseは自動的に1と0に読み替えられるので、わざわざ数値に置き換える処理を行う必要はありません。
|
1 2 3 4 5 6 7 8 9 10 11 |
[In ]: #混同行列、正解率、適合率、再現率、F値を表示 print('confusion matrix = \n', confusion_matrix(y_true = Y_test, y_pred = Y_pred)) print('accuracy = ',accuracy_score(y_true = Y_test , y_pred = Y_pred)) print('precision = ',precision_score(y_true = Y_test , y_pred = Y_pred)) print('recall = ',recall_score(y_true = Y_test , y_pred = Y_pred)) print('f1 score = ',f1_score(y_true = Y_test , y_pred = Y_pred)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
[Out ]: confusion matrix = [[211 0] [ 7 1]] accuracy = 0.9680365296803652 precision = 1.0 recall = 0.125 f1 score = 0.2222222222222222 |
各種評価指標を算出して表示しました。混同行列を見ると、訓練データには8つのPositiveが含まれていたようです。しかし、真陽性はわずか1であるのに対し、偽陰性が7であることがわかります。つまり、訓練データがNegativeに大きく偏っていたため、このモデルではテストデータをNegativeに分類し過ぎてしまっているのです。ゆえに、recallやf1scoreが非常に小さくなっています。一方、accracyの値が先ほどの実装よりもむしろ大きくなっている点から、accuracyが偏りのあるデータに対する予測を評価する際に有効ではない場合があることがわかります。次に、ROC曲線とPR曲線を描き、それぞれのAUCを求めます。
|
1 2 3 4 5 6 7 8 |
[In ]: #ROC曲線を描くために必要な要素を、検証データがクラス1に属する予測確率から計算 Y_score = lr.predict_proba(X_test)[:,1] fpr, tpr, thresholds = roc_curve(y_true=Y_test,y_score=Y_score) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
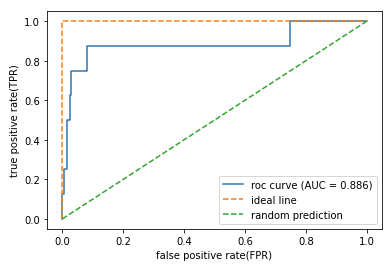
[In ]: #ROC曲線を描き、AUCを算出 plt.plot(fpr,tpr,label='roc curve (AUC = %0.3f)' % auc(fpr,tpr)) plt.plot([0,0,1], [0,1,1], linestyle='--', label='ideal line') plt.plot([0, 1], [0, 1], linestyle='--', label='random prediction') plt.legend() plt.xlabel('false positive rate(FPR)') plt.ylabel('true positive rate(TPR)') plt.show() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
[In ]: #PR曲線を描き、AUCを算出 probas_pred = lr.predict_proba(X_test)[:,1] precision, recall, thresholds = precision_recall_curve(y_true=Y_test, probas_pred=Y_score) plt.plot(recall,precision,label='precision_recall_curve (AUC = %0.3f)' % auc(recall,precision)) plt.plot([0,1], [1,1], linestyle='--', label='ideal line') plt.legend() plt.xlabel('recall') plt.ylabel('precision') plt.show() |
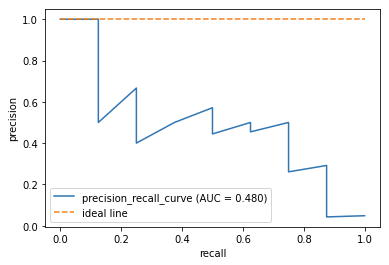
二つの曲線とそれぞれのAUCを見比べてみてください。このように、大きな偏りがあるデータに対しての予測の場合は、ROC曲線のAUCはそれほど小さくならないのに対し、PR曲線のAUCは少ない予測ミスにも敏感に反応して大きく値を低下させます。これらの図から、偏りのあるデータに対する分類予測を評価するときは、PR曲線のAUCが有効であることがお分りいただけたことでしょう。
まとめ
いかがでしたでしょうか。本稿を通して、分類問題に対する機械学習の評価指標について理解を深められていたら幸いです。本稿では、分類問題に対する機械学習の評価指標を扱いましたが、同様に、回帰に関しても評価指標が存在します。機械学習のモデルを適切に評価して最適なモデルを選べるように、本稿の内容と併せて学習していきましょう。
機械学習を始めようと考えている方は下記の無料コースもお勧めです。ぜひ、受講をお待ちしております。
機械学習 準備編 無料講座



