scikit-learn 入門：6つの機能と分類・回帰の実装方法を徹底解説！

皆さんは、scikit-learn（よみ：サイキット・ラーン）をご存知でしょうか。Pythonを使っている方、機械学習を学ばれている方なら一度は耳にしたことがあることでしょう。しかし、scikit-learnを知っている方の中でも、scikit-learnでいったい何ができるのか、その全貌を知っている方はそれほど多くはないのではないでしょうか。

そこで本稿では、scikit-learnの4つの特徴と、6つの主な機能について詳しく解説した上で、実際に回帰と分類の実装を行います。機械学習をこれから学ぼうとされている方はもちろん、scikit-learnを使っている皆さんも改めて、本稿でscikit-learnの良さを学びましょう。

scikit-learnとは

まずは、scikit-learnとはいったいどのようなライブラリで、どのような特徴があるのかを解説していきます。

scikit-learnの概要

scikit-learnは、オープンソースの機械学習ライブラリです。2007年にGoogle Summer of Code projectとしてDavid Cournapeau氏によって開発が始められ、今日でも国際的なコミュニティーの元で開発が続けられています。Numpy、SciPy、matplotlibといったPythonのライブラリ上で動作し、scikit-learnを使えば、誰でも手軽に機械学習の前処理やモデリング、評価指標の算出などを行うことができます。

scikit-learnの４つの特徴

次に、scikit-learnの４つの特徴について、詳しく説明していきます。なお、ここで説明する４つの特徴については、後半の実装の際にも再度確認します。

①アルゴリズムが豊富かつ使いやすい

１つ目の特徴は、アルゴリズムが豊富に用意されており、かつ使いやすいという点です。scikit-learnには、回帰、分類、クラスタリング、次元削減など、あらゆる分野のアルゴリズムが揃っています。また、同じ分野のアルゴリズムは実装の際のコードに共通性があり、様々なアルゴリズムを容易に使い分けることができるようになっています。

②アルゴリズムチートシートを参考に、簡単に適切な手法を選択できる

２つ目の特徴は、チートシートを参考にして簡単にアルゴリズムを選択できる点です。用意されているアルゴリズムがどれだけ豊富でも、どの手法を用いればいいのか分からなければ意味がありませんね。しかし、アルゴリズムのメカニズムは複雑であるため、どの手法を用いるのが適切なのかを知るためにあらゆる手法について詳しく学んでいては、いつまでたっても機械学習を実践することはできないでしょう。そんな悩みを解決してくれるのが下のアルゴリズムチートシートです。

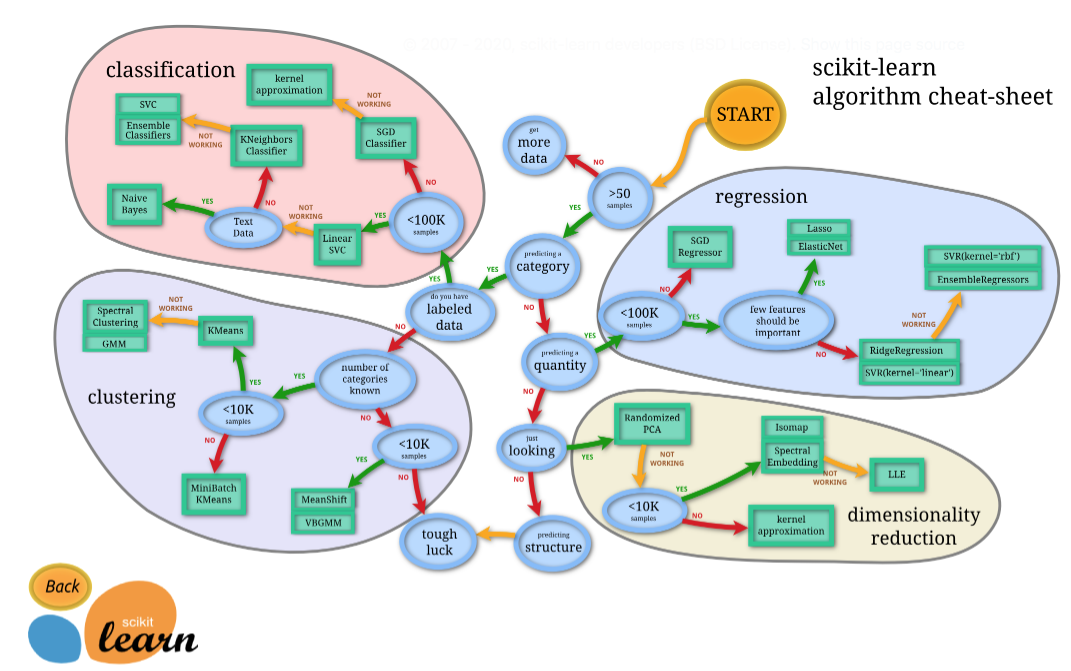
<scikit-learn公式より＞

右上の「START」から、用いるデータの特徴に関するYesかNoの二択の選択肢を辿っていくと、データに合ったアルゴリズムを選択することができます。このチートシートを使うことで、全てのアルゴリズムに精通していなくても、機械学習の実装を試しながら学んでいくことができます。（※チートシートでは、scikit-learn内のアルゴリズムの一部しか紹介されていません。ゆえに、ある程度適切ではあるものの最適なアルゴリズムではない可能性があります。各分野のアルゴリズムの知識が付いてきたら自分で適切な手法を選択するようにしましょう。）

③サンプルのデータセットが用意されている

３つ目の特徴は、scikit-learnにはサンプルのデータセットが用意されている点です。機械学習を始める前に、学習に用いるデータを用意しなければいけません。今日では、多くのデータセットがインターネット上で公開されているため、それらを活用するというのも一つの手段ではあります（参考：機械学習データセット24選！）。しかし、整形されたデータですぐに機械学習を実装してみたい場合もあるでしょう。そんな時には、scikit-learnに用意されているデータセットを使うことをお勧めします。scikit-learnに用意されているデータセットは使いやすいように整形されているため、前処理に余計な手間がかかりません。また、ボストンの住宅価格、アヤメの種類、糖尿病患者、手書き数字など、様々な種類のデータが用意されているため、試してみたいアルゴリズムに合わせてデータを選択することも可能になっています。＜参考： [ 公式 ]scikit-learnのデータセット一覧(英語)＞

④公式サイトの解説が丁寧で便利

公式Webサイトの解説が非常に丁寧で便利であることも、scikit-learnの特徴の一つと言えるでしょう。ユーザーガイドには、scikit-learnの各アルゴリズムについて、仕組みや各モジュール・各クラスごとの引数の解説、実装例などが載せられています。これを参照すればオーソドックスな使い方はスムーズに習得できるでしょう。

scikit-learnの６つの機能

scikit-learnとはどのようなライブラリで、どのような特徴があるのかお分かりいただけたでしょうか。本節では、scikit-learnの６つの具体的な機能について、機械学習の知識に関する解説も交えながらご説明します。

回帰

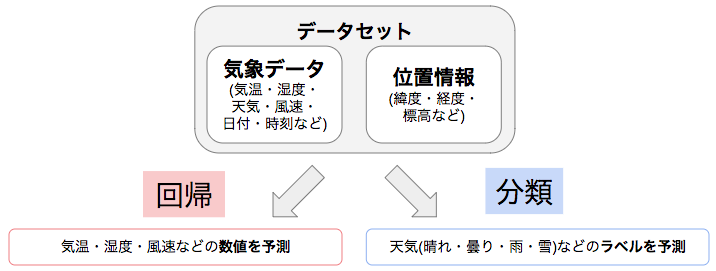
１つ目の機能が回帰です。回帰とは、二種類ある教師あり学習のうちの一つで、データセットを学習して新たな入力に対する出力の数値を予測する手法のことです。例えば、過去の気象データと位置情報を学習し、その地点の翌日の気温を予測する際には回帰を行います。また、本稿後半の実装では、ボストンの住宅価格のデータセットを用いて、町の犯罪率や高速道路へのアクセスの良さなどのデータから土地の住宅価格を予測する回帰を行います。

分類

２つ目の機能が分類です。分類はもう一つの教師あり学習で、データを学習して、新たな入力に対する出力のラベルを予測する手法のことです。回帰と同様に気象に関して例えるならば、過去の気象データと位置情報を学習し、その地点の翌日の天気（晴れ、曇り、雨、雪）を予測するのは、分類です。また、本稿の後半では、アヤメのデータセットを用いて、アヤメの花びらやがくの大きさから、そのアヤメがどの種類なのかを予測する分類を行います。

クラスタリング

３つ目の機能は教師なし学習のクラスタリングです。クラスタリングとは、データの特徴から関連の深いデータや似通ったデータを見つけ、クラスターに分ける（＝グルーピングする）手法です。例えば、企業の購買データの分析などに応用されていて、クラスタリングの結果に基づいて顧客に商品をレコメンドすることもあります。scikit-learnでは、クラスタリングもK-meansをはじめ数多くのアルゴリズムで実行可能です。

次元削減

４つ目の機能は次元削減です。次元削減は教師なし学習の一種です。データセットの特徴量同士の関係を学習し、より簡潔かつ効率的に特徴量の情報を表現することなどを目的に、新たな特徴量を計算で導出して特徴量の数を削減する手法です。例えば、近年盛んに様々なメディアで取り上げられているビッグデータを処理する際に、データセットのあまりの大きさにコンピュータの処理性能が不足することがあります。そういった場合に、次元削減をすることでコンピュータの性能不足を補うことができます。scikit-learnでは、主成分分析や因子分析などで次元削減を行うことができます。

データの前処理

５つ目の機能はデータの前処理です。データの前処理といっても、pandasで行うようなデータの整形ではなく、機械学習が正しく実行されるためのデータの数値変換を行います。適切な前処理を行うことで、特定の特徴量が学習結果に過大な影響を与えることなどを防ぐことができます。例えば、データの平均を０、標準偏差を１にする標準化などを行います。なお、scikit-learnでは他にも、非線型変換や正規化、離散化などの処理を行うことができます。

モデルの評価と選択

scikit-learnを使うための準備

次に、scikit-learnを使うための準備について、簡単にご説明します。

pipでインストールする場合

パッケージマネージャーのpipを用いる場合、WindowsユーザーもMacユーザーも、手順は同じです。まず、Pythonの公式サイトからPythonをインストールしましょう。そのあと、ターミナル（Windowsの場合はコマンドプロンプト）に

pip install -U scikit-learn

と入力することでscikit-learnをPythonで使うことができます。なお、

python -m pip show scikit-learn

と入力した際にscikit-learnのバージョンとインストール先が表示されれば、インストールは正常に完了しています。

Google Colabの場合

インストールするよりもお手軽にscikit-learnを使ってみたい方には、Google Colabがおすすめです。Google Colabにはscikit-learnが元から用意されているため、ノートブックを作成したらすぐに利用可能です。（参考：Google Colabの使い方）

なお、pipではなくcondaでPCにインストールしたい方や、Linuxをご利用の方は、scikit-learn公式サイトをご確認ください。

scikit-learnによる機械学習実装

いよいよ、scikit-learnを用いた機械学習の実装に取り掛かります。本稿では、皆さんにscikit-learnで実装可能な機械学習手法の豊富さや、チートシートの利便性、scikit-learnに用意されているデータセットの内容について知っていただくため、以下のような流れで実装を行います。

0. ライブラリ・データセットの準備

1. 分類の実装（iris(アヤメ)データセット）

2. 回帰とモデル選択の実装（ボストン住宅価格データセット）

まずは、ライブラリとデータセットの準備から行いましょう。

ライブラリ・データセットの準備

本稿の実装では、pandasとscikit-learnを用います。pandasは効率的にデータを処理・整形するためのライブラリです。また、scikit-learnから、本稿の実装で用いるアヤメ(iris)のデータセットと、ボストンの住宅価格のデータセットをインポートしておきましょう。

分類の実装（iris(アヤメ)データセット）

アヤメの種類に関するデータセットで、アヤメの種類の予測を行います。まずは、データを読み込んで中身を確認した後に、訓練データとテストデータに分割しましょう。

データの確認と分割

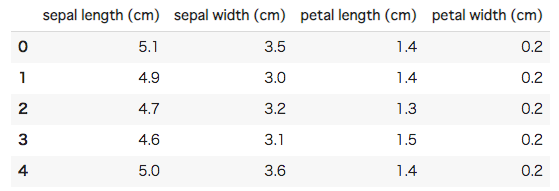
特徴量の最初の五行を表示してみました。sepalというのが「がく」で、petalというのが「花弁（花びら）」に当たります。がくと花弁それぞれの長さと幅から、アヤメの種類を当てる分類問題を解くためのデータセットになっています。

次に、特徴量の基本統計量を確認しましょう。

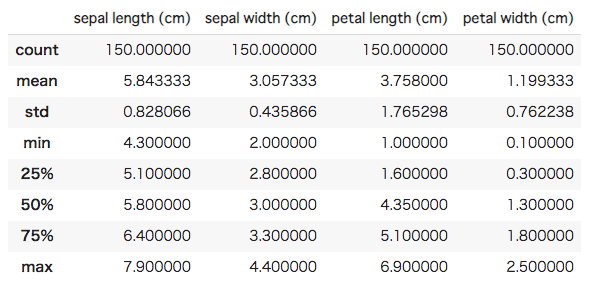
上記の表では、上から順にデータ数、平均値、標準偏差、最小値、第１四分位数、中央値、第3四分位数、最大値が表示されています。これらの情報から、データに対して具体的なイメージを持つことができ、明らかにおかしいデータが含まれていないかを確認することもできます。さらに、特徴量に欠損値がないかも一応確認してみましょう。

基本統計量を表示した際にcount（データ数）が全て150だったことから予想はつきましたが、やはり欠損値はないようです。このように、扱いやすくデータが整形されているのもサンプルデータセットの特徴です。それでは、ラベルも確認してみましょう。

0、1、2のラベルがそれぞれ50ずつあるようですね。これらの数字はそれぞれがアヤメの種類に対応しています。

データセットの中身が確認できたところで、model_selectionモジュールのtrain_test_splitメソッドを用いて、データを訓練データとテストデータに分割しましょう。train_test_splitの引数には、前から順に特徴量、ラベル、テストデータにする割合、再現性を持たせるため乱数生成のシードを指定するrandom_state引数を入力します。

分割した訓練データとテストデータの構造を確認してみましょう

特徴量は75行4列、ラベルは75行1列に分割できていることがわかります。

分類のモデル実装

いよいよ、分類のためのモデルを実装していきます。と言っても、選べるモデルは非常に豊富であるため、ここでは先ほどご紹介したチートシートを活用してみましょう。

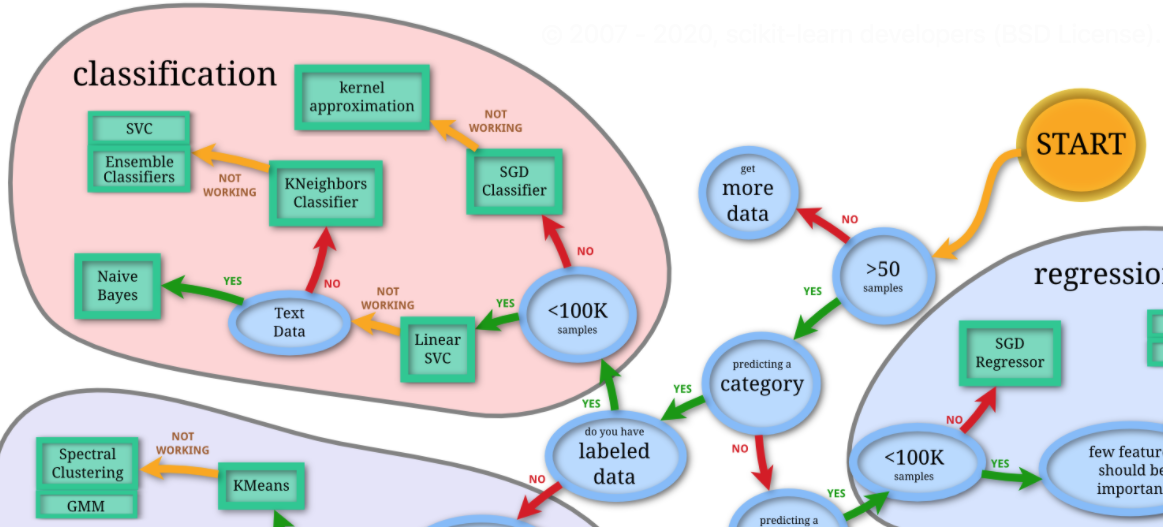
右上のSTARTから順に辿っていくと、今回の場合はSTART→Yes→Yes→Yes→Yesとなり、Linear SVCが推奨されました。早速svm（サポートベクターマシン）モジュールをインポートし、LinearSVCクラスのインスタンスを作成してfitメソッドで学習させましょう。先ほどのデータの分割と同様に、何回やっても、どの環境で実行しても結果が同じになるように、インスタンス作成時にrandom_state引数を指定します。また最大のイテレーション回数を指定するmax_iter引数へ3000と指定します。

モデルにデータを学習させたので、アヤメの種類を予測します。予測には、LinearSVCのインスタンスのpredictメソッドを用います。

無事に予測ができましたが、試しにチートシート上でLinearSVCがうまく予測できない場合に推奨されているK近傍法(Kneighbor)と、オーソドックスな分類手法であるロジスティック回帰モデル（LogisticRegression）でもそれぞれ分類予測を行います。先ほどのLinearSVCでの分類予測とコードが類似している点にもご注目ください。

3つのモデルで予測ができたので、今度はそれぞれの予測モデルの性能を比較してみましょう。そのための評価指標として、今回は正解率(accuracy)を用い、混同行列と併せて表示します。正解率は、全ての予測のうち、正しく分類できていた予測の割合を表します。また、混同行列は、実際のラベルと予測のラベルを行列形式で表示したものです。（混同行列や分類問題におけるその他の評価指標について詳しく知りたい方は、評価指標の記事も併せてご覧ください。）

この混同行列は、左上から右下への対角線上に位置する要素が正解した予測の数になっています。正解率と合わせてみても、今回の分類ではK近傍法が最もうまく予測できていると言えそうです。K近傍法はオーソドックスなロジスティック回帰モデルと比べても性能がよかったことから、チートシートの有用性をお分かりいただけるかと思います。

回帰とモデル選択の実装（ボストン住宅価格データセット）

次に、ボストンの住宅価格に関するデータセットを用いて、回帰を行い、住宅価格を予測します。さらに、モデル選択についての手法であるクロスバリデーションも適用します。まずは、先ほどと同様にデータの中身を確認したあと、訓練データとテストデータに分割します。

データの確認

データセットの読み込みと、最初の5行の表示から始めましょう。

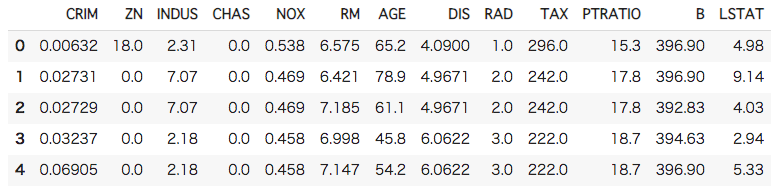
先ほどよりも特徴量が多く、数値の単位も様々であることがわかります。それぞれの変数の意味は以下の通りです。

• CRIM 町の人口あたり犯罪率
• ZN 25000平方フィート以上の住宅地の割合
• INDUS 町ごとの非小売業の土地の割合
• CHAS Charles川に関するダミー変数(川に接していたら1、そうでなければ0)
• NOX 一酸化窒素濃度（1000万分の1）
• RM 住居当たりの平均部屋数
• AGE 1940年より前に建設された物件の割合
• DIS ボストンの5つの雇用センターまでの重み付けされた距離
• RAD 放射状高速道路へのアクセスしやすさ
• TAX 10000ドル当たりの固定資産税総額
• PTRATIO 町ごとの生徒と教師の比率
• B   1000(Bk – 0.63)^2 ※Bkは町の黒人比率
• LSTAT 低所得の人々の割合

次に、基本統計量を表示して全体像を掴みましょう。

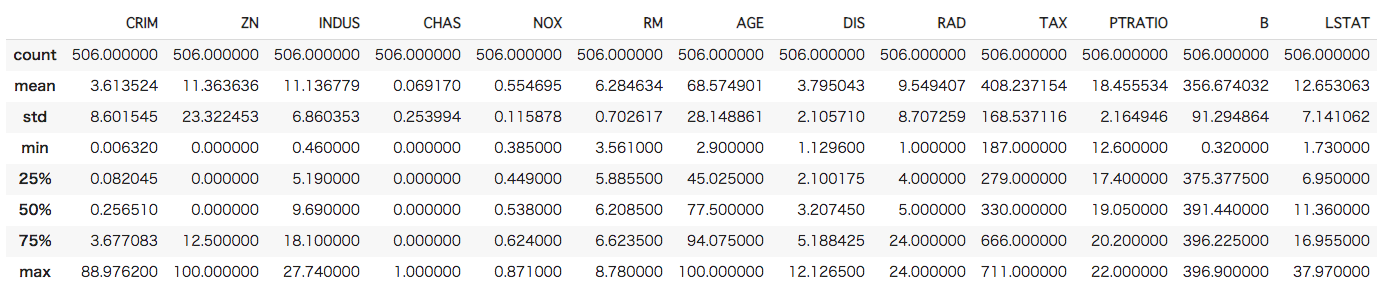
犯罪率や住宅地比率だけをみても、町ごとの性質に大きな差があることがわかります。このデータでも一応欠損値の有無を確認しておきましょう。

やはり欠損値はありません。スムーズに学習に入れるため非常にありがたいですね。次に、ターゲットをpandasのSeriesというデータ構造に格納して基本統計量を確認します。

こちらも、最小値と最大値で１０倍もの差がありますね。グラフにしてみても面白いですが、本稿では割愛します。Pythonでの可視化については、seabornの記事で詳しく解説していますので、ぜひご覧ください。最後に、先ほどと同様にデータを学習データとテストデータに分割します。

回帰のモデル実装

では、回帰のモデルを実装していきましょう。回帰でも、チートシートを参考にアルゴリズムを選択します。

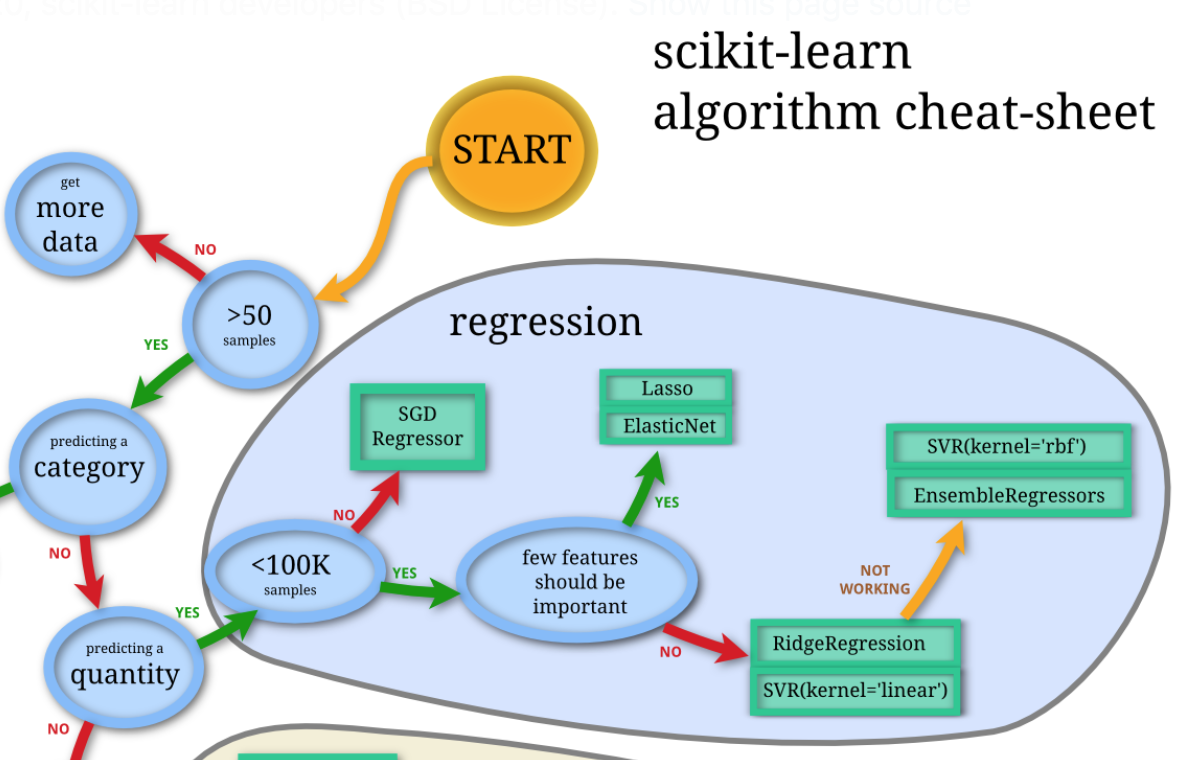
今度はSTART→Yes→No→Yes→Yesとなりfew features should be important(少数の特徴量が重要である)まで来ました。この質問に関しては、データを確認しただけでは判断がつかないため、YesとNoの先のアルゴリズムからひとつずつ、LassoとRidgeRegressionを選んで実装することとします。また、参考に通常の線形回帰モデルでも予測を行います。なお、本稿では、各アルゴリズムのインスタンスを作成する際の引数には、scikit-learnの公式サイトで紹介されている例を参考に、同じ値を入れることとします。各アルゴリズムの引数についてより詳しく知りたい方は、scikit-learn公式サイトをご確認ください。

3つのモデルで予測ができたところで、モデルの性能を評価するために評価指標を計算します。ここでは、決定係数を用いることとします。なお、決定係数とは、簡単に言えば「実際の値のうち予測モデルで説明できた割合」を表す評価指標で０〜１の範囲で変動し、大きければ大きいほどモデルの性能がいいということになります。

今回は、モデル間で性能に大差はないという結果になりました。線形モデルが最も性能が良かったですが、チートシートにしたがって用いた二つのモデルもまずまずの性能を出せたと言えるでしょう。

モデルの評価と選択：クロスバリデーション（交差検証）　の実装

ここまで、scikit-learnの機能のうち、「分類」と「回帰」の実装について解説して来ました。ここでは、もうひとつの機能を簡単に実装してみたいと思います。それは、「モデルの評価と選択」のための機能です。実をいうと、データセットの訓練データ・テストデータへの分割や、分類の評価のところで表示した混同行列もこの機能によるものです。ここではクロスバリデーション（交差検証）という手法をご紹介します。

クロスバリデーションとは、データセットを訓練データとテストデータに分割してモデルに学習させてスコアを出すというプロセスを複数回繰り返し、全てのスコアの平均で性能を測ることで、より一般的な予測性能が高いモデルを選択するという手法です。例えば先ほどの回帰の例でいうと、この手法を用いることで、たまたまLassoモデルには不利な形でデータセットが分割されたためにLassoモデルの性能が低くなってしまったというケースを回避できる可能性が高まります。

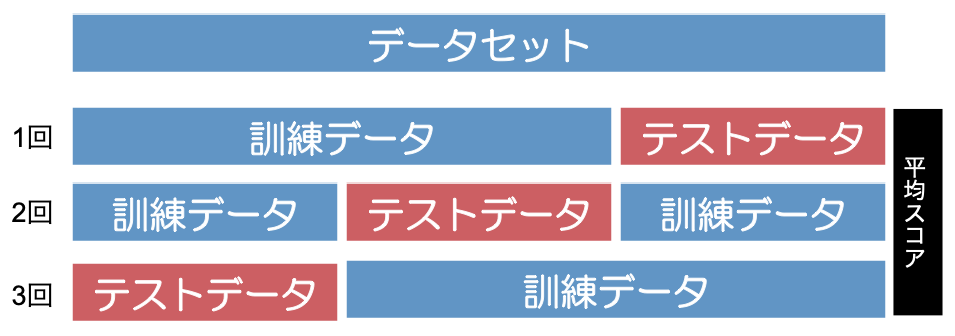
では、繰り返しの回数を5回に設定してクロスバリデーションを実装してみましょう。まずはLassoモデルでクロスバリデーションを行います。

この結果から、データの分割の仕方によって結果が大きく変動していることがわかりますね。では、次にRidgeモデル、線形モデルについても同様にクロスバリデーションを行います。

以上の結果から、今回の分類に関しては、Ridgeモデル、線形モデルの方がLassoモデルよりも優れていることを確認できました。なお、ここではクロスバリデーションについて紹介しましたが、モデルの評価と選択のための手法は他にもあります。こちらの記事ではハイパーパラメータチューニングという手法についてまとめてありますので、併せてご覧ください。

まとめ

いかがでしたでしょうか。scikit-learnの基本的な使い方はお分かりいただけたかと思いますが、本稿でご紹介したscikit-learnの機能はほんの一部にすぎません。scikit-learnを使いこなせるようになれば基本的な機械学習の実装は扱えると思うので、公式サイトも頼りに色々な手法を試してみてください。

また、機械学習で用いられている数学や統計の基礎について学びたい方には、こちらの無料コースがオススメです。

• 線形代数入門
• 統計入門（前編）

さらに、それぞれの機械学習アルゴリズムについてより詳しく学びたいという方は、ぜひ、以下のコースをご利用ください。

• 線形回帰入門、実践 線形回帰
• ロジスティック回帰
• 決定木とランダムフォレスト
• サポートベクターマシン
• ナイーブベイズ